Volatility smile
see chapter 18 in Hull, Options, Futures, and other Derivatives
Given that the Call-Put-Parity holds, all
options, whether calls or puts,
should be of the same price. As price we mean the implied volatility of the
option if we solve the Black-Scholes-Merton formula for the volatility parameter
given all other parameters (interest rate, time to maturity, market price, ..)
known. This volatility is implied by the prices of the options and therefore
called implied volatility.
Under the non-arbitrage argument the prices of puts and calls should be the same. However, as we compare market prices of such options and solve the BSM formula for the implied volatility we observe significant deviation from zero difference.
TODO: [ here follows a picture ]
Smile
One argument for the SMILE is that the Black-Scholes-Merton formula implies a static volatility whereas in real world this is certainly to move every day. Another argument is that the BSM formula depends on lognormal distributed returns whereas real world options’ returns deviate from this distribution. Empirically it has been shown that the lognormal distribution underestimates the heavy tails and thus the occurrence of rare events. This would enable an arbitrageur to collect a premium if she would buy deep out of the money put and call options as these are priced too cheap. On the rare event it will pay off.
Smirk
The implied volatilities of puts and calls having the same degree of moneyness can also deviate. In this situation we call the volatility smile a smirk as it is left skewed.
[ here follows a picture ]
Reasons for this can be that shorting of the underlying instrument can be more expensive or simply, investors afford more to protect the downside risk.
Volatility Surface
We can draw the implied volatility against moneyness (i.e. ) and time to maturity.
ivsurf = [
14.2, 13.0, 12.0, 13.1, 14.5;
14.0, 13.0, 12.0, 13.1, 14.2;
14.1, 13.3, 12.5, 13.4, 14.3;
14.7, 14.0, 13.5, 14.0, 14.8;
15.0, 14.4, 14.0, 14.5, 15.1;
14.8, 14.6, 14.4, 14.7, 15.0 ];
surf(ivsurf);
set(gca, 'XTickLabel', [0.9, 0.95, 1, 1.05, 1.1]);
set(gca, 'YTickLabel', ['1m'; '3m'; '6m'; '1y'; '2y'; '5y']);
set(gca, "view", [48, 44]);
print('volasurf_ch18.ps','-dpsc2');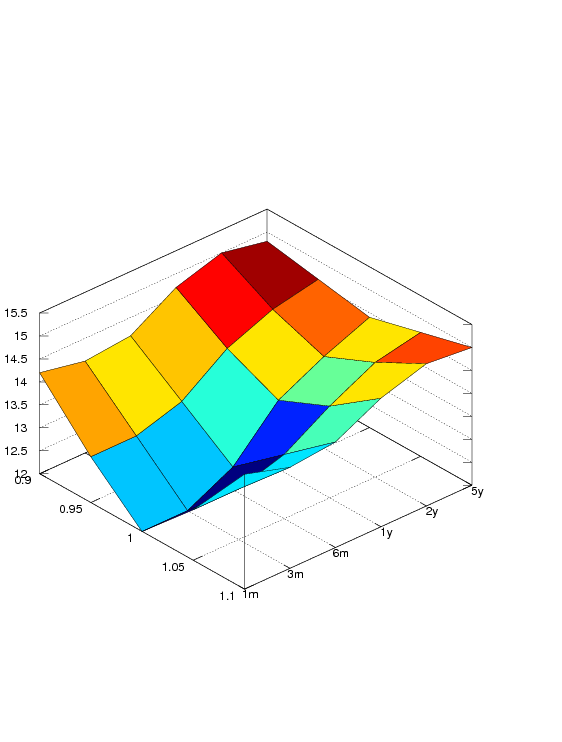
From a set of priced options (both puts and calls) we can derive their implied volatilities. Using some interpolation on the grid of moneyness, time to maturity we calculate the surface of expected implied volatilities.